2016年高考全國卷新課標三理科數(shù)學試題解析(word版)
2016年普通高等學校招生全國統(tǒng)一考試
理科數(shù)學
注意事項:
1.本試卷分第Ⅰ卷(選擇題)和第Ⅱ卷(非選擇題)兩部分。第Ⅰ卷1至3頁,第Ⅱ卷3至5頁。
2.答題前,考生務必將自己的姓名、準考證號填寫在本試題相應的位置。
3.全部答案在答題卡上完成,答在本試題上無效。
4. 考試結束后,將本試題和答題卡一并交回。
第Ⅰ卷
選擇題:本大題共12小題,每小題5分,在每小題給出的四個選項中,只有一項是符合
題目要求的。

試題分析:由題意,得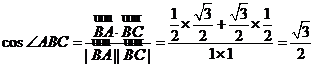 ,所以
,所以![]() ,故選A.
,故選A.
考點:向量夾角公式.
(4)某旅游城市為向游客介紹本地的氣溫情況,繪制了一年中月平均最高氣溫和平均最低氣溫的雷達圖。
圖中A點表示十月的平均最高氣溫約為150C,B點表示四月的平均最低氣溫約為50C。下面敘述不正確的是
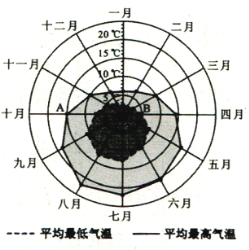
(A) 各月的平均最低氣溫都在00C以上 (B) 七月的平均溫差比一月的平均溫差大
(C) 三月和十一月的平均最高氣溫基本相同 (D) ![]() 平均氣溫高于200C的月份有5個
平均氣溫高于200C的月份有5個
【答案】D

考點:1、平均數(shù);2、統(tǒng)計圖



(A)3 (B)4 (C)5 (D)6
【答案】B

考點:程序框圖.
(8)在![]() 中,
中,![]() ,BC邊上的高等于
,BC邊上的高等于![]() ,則
,則![]()
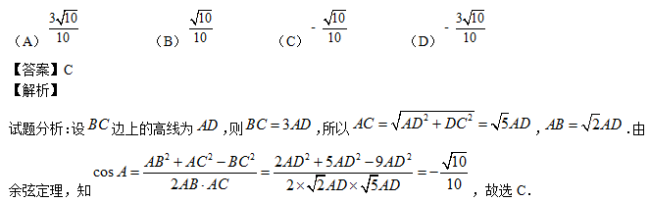
考點:余弦定理.
(9)如圖,網(wǎng)格紙上小正方形的邊長為1,粗實現(xiàn)畫出的是某多面體的三視圖,則該多面體的表面積為

(A)![]() (B)
(B)![]() (C)90 (D)81
(C)90 (D)81
【答案】B

考點:空間幾何體的三視圖及表面積.
(10) 在封閉的直三棱柱![]() 內(nèi)有一個體積為V的球,若
內(nèi)有一個體積為V的球,若![]() ,
,![]() ,
,![]() ,
,![]() ,
,
則V的最大值是
(A)4π (B)![]() (C
(C![]() )6π (D)
)6π (D)![]()
【答案】B
【解析】
試題分析:要使球的體積![]() 最大,必須球的半徑
最大,必須球的半徑![]() 最大.由題意知球的與直三棱柱的上下底面都相切時,球的半徑取得最大值
最大.由題意知球的與直三棱柱的上下底面都相切時,球的半徑取得最大值![]() ,此時球的體積為
,此時球的體積為![]() ,故選B.
,故選B.
考點:1、三棱柱的內(nèi)切球;2、球的體積.
(11)已知O為坐標原點,F(xiàn)是橢圓C:![]() 的左焦點,A,B分別為C的左,右頂點.P
的左焦點,A,B分別為C的左,右頂點.P
為C上一點,且![]() 軸.過點A的直線l與線段
軸.過點A的直線l與線段![]() 交于點M,與y軸交于點E.若直線BM經(jīng)過OE的中
交于點M,與y軸交于點E.若直線BM經(jīng)過OE的中
點,則C的離心率為
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
【答案】A

考點:橢圓方程與幾何性質(zhì).
(12)定義“規(guī)范01數(shù)列”{an}如下:{an}共有2m項,其中m項![]() 為0,m項為1,且對任意
為0,m項為1,且對任意![]() ,
,![]()
中0的個數(shù)不少于1的個數(shù).若m=4,則不同的“規(guī)范01數(shù)列”共有
(A)18個 (B)16個 (C)14個 (D)12個
【答案】C
【解析】
試題分析:由題意,得必有![]() ,
,![]() ,則具體的排法列表如下:
,則具體的排法列表如下:
0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
1 | 0 | 1 | 1 | ||||
1 | 0 | 1 | |||||
| 1 | 0 | ||||||
1 | 0 | 0 | 1 | 1 | |||
1 | 0 | 1 | |||||
| 1 | 0 | ||||||
1 | 0 | 0 | 1 | ||||
| 1 | 0 | ||||||
1 | 0 | 0 | 0 | 1 | 1 | ||
1 | 0 | 1 | |||||
| 1 | 0 | ||||||
1 | 0 | 0 | 1 | ||||
| 0 |
考點:計數(shù)原理的應用.![]()
![]()
第II卷
本卷包括必考題和選考題兩部分。第(13)題~第(21)題為必考題,每個試題考生都必須作答。第(22)題~第(24)題未選考題,考生根據(jù)要求作答。
二、填空題:本大題共3小題,每小題5分
(13)若![]() 滿足約束條件
滿足約束條件 則
則![]() 的最大值為_____________.
的最大值為_____________.
【答案】![]()

考點:簡單的線性規(guī)劃問題.
(14)函數(shù)![]() 的圖像可由函數(shù)
的圖像可由函數(shù)![]() 的圖像至少向右平移_____________個
的圖像至少向右平移_____________個
單位長度得到.
【答案】![]()
【解析】
試題分析:因為![]() ,
,![]() =
=
![]() ,所以函數(shù)
,所以函數(shù)![]() 的圖像可由函數(shù)
的圖像可由函數(shù)![]() 的圖像至少向右平移
的圖像至少向右平移![]() 個單位長度得到.
個單位長度得到.
考點:1、三角函數(shù)圖象的平移變換;2、兩角和與差的正弦函數(shù).
(15)已知![]() 為偶函數(shù),當
為偶函數(shù),當![]() 時,
時,![]() ,則曲線
,則曲線![]() 在點
在點![]() 處的切線方程
處的切線方程
是_______________。
【答案】![]()

考點:1、函數(shù)的奇偶性與解析式;2、導數(shù)的幾何意義.
(16)已知直線![]() :
:![]() 與圓
與圓![]() 交于
交于![]() 兩點,過
兩點,過![]() 分別做
分別做![]() 的垂線與
的垂線與![]() 軸
軸
交于![]() 兩點,若
兩點,若![]() ,則
,則![]() __________________.
__________________.
【答案】4
【解析】
試題分析:因為![]() ,且圓的半徑為
,且圓的半徑為![]() ,所以圓心
,所以圓心![]() 到直線
到直線![]() 的距離為
的距離為![]() ,則由
,則由![]() ,解得
,解得![]() ,代入直線
,代入直線![]() 的方程,得
的方程,得![]() ,所以直線
,所以直線![]() 的傾斜角為
的傾斜角為![]() ,由平面幾何知識知在梯形
,由平面幾何知識知在梯形![]() 中,
中,![]() .
.
考點:直線與![]() 圓的位置關系.
圓的位置關系.
三、解答題:解答應寫出文字說明,證明過程或演算步驟.
(17)(本小題滿分12分)
已知數(shù)列![]() 的前n項和
的前n項和![]() ,其中
,其中![]() .
.
(I)證明![]() 是等比數(shù)列,并求其通項公式;
是等比數(shù)列,并求其通項公式;
(II)若![]() ,求
,求![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】

考點:1、數(shù)列通項![]() 與前
與前![]() 項和為
項和為![]() 關系;2、等比數(shù)列的定義與通項及前
關系;2、等比數(shù)列的定義與通項及前![]() 項和為
項和為![]() .
.
(18)(本小題滿分12分)
下圖是我國2008年至2014年生活垃圾無害化處理量(單位:億噸)的折線圖

(I)由折線圖看出,可用線性回歸模型擬合y與t的關系,請用相關系數(shù)加以說明;
(II)建立y關于t的回歸方程(系數(shù)精確到0.01),預測2016年我國生活垃圾無害化處理量。
參考數(shù)據(jù):![]() ,
,![]() ,
, ,≈2.646.
,≈2.646.
參考公式:相關系數(shù)
回歸方程![]() 中斜率和截距的最小二乘估計公式分別為:
中斜率和截距的最小二乘估計公式分別為:
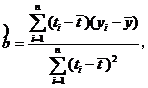
![]()
【答案】(Ⅰ)理由見解析;(Ⅱ)1.82億噸.

(Ⅱ)由![]() 及(Ⅰ)得
及(Ⅰ)得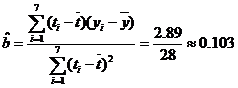 ,
,
![]() .
.
所以,![]() 關于
關于![]() 的回歸方程為:
的回歸方程為:![]() .
.
將2016年對應的![]() 代入回歸方程得:
代入回歸方程得:![]() .
.
所以預測2016年我國生![]() 活垃圾無害化處理量將約1.82億噸.
活垃圾無害化處理量將約1.82億噸.
考點:線性相關與線性回歸方程的求法與應用.
(19)(本小題滿分12分)
如圖,四棱錐![]() 中,
中,![]() 地面
地面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為線段
為線段![]() 上一點,
上一點,![]() ,
,![]() 為
為![]() 的中點.
的中點.
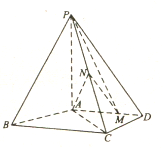
(I)證明![]() 平面
平面![]() ;
;
(II)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)見解析;(Ⅱ)![]() .
.




考點:1、拋物線定義與幾何性質(zhì);2、直線與拋物線位置關系;3、軌跡求法.
(21)(本小題滿分12分)
![]() 設函數(shù)
設函數(shù)![]() ,其中
,其中![]() ,記
,記![]() 的最大值為
的最大值為![]() .
.
(Ⅰ)求![]() ;
;
(Ⅱ)求![]() ;
;
(Ⅲ)證明![]() .
.


考點:1、三角恒等變換;2、導數(shù)的計算;3、三角函數(shù)的有界性.
請考生在[22]、[23]、[24]題中任選一題作答。作答時用2B鉛筆在答題卡上把所選題目題號后的方框涂黑。如果多做,則按所做的第一題計分。
22.(本小題滿分10分)選修4-1:幾何證明選講
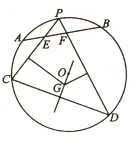
如圖,⊙O中![]() 的中點為
的中點為![]() ,弦
,弦![]() 分別交
分別交![]() 于
于![]() 兩點.
兩點.
(I)若![]() ,求
,求![]() 的大小;
的大小;
(II)若![]() 的垂直平分線與
的垂直平分線與![]() 的垂直平分線交于點
的垂直平分線交于點![]() ,證明
,證明![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)見解析.
;(Ⅱ)見解析.

考點:1、圓周角定理;2、三角形內(nèi)角和定理;3、垂直平分線定理;4、四點共![]() 圓.
圓.
23.(本小題滿分10分)選修4-4:坐標系與參數(shù)方程
在直角坐標系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() ,以坐標原點為極點,以
,以坐標原點為極點,以![]() 軸的正半軸為極軸,,建立極坐標系,曲線
軸的正半軸為極軸,,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(I)寫出![]() 的普通方程和
的普通方程和![]() 的直角坐標方程;
的直角坐標方程;
(II)設點P在![]() 上,點Q在
上,點Q在![]() 上,求|PQ|的最小值及此時P的直角坐標.
上,求|PQ|的最小值及此時P的直角坐標.
【答案】(Ⅰ)![]() 的普通方程為
的普通方程為![]() ,
,![]() 的直角坐標方程為
的直角坐標方程為![]() ;(Ⅱ)
;(Ⅱ)![]() .
.

考點:1、橢圓的參數(shù)方程;2、直線的極坐標方程.
24.(本小題滿分10分)選修4-5:不等式選講
已知函數(shù)![]()
(I)當a=2時,求不等式![]() 的解集;
的解集;
(II)設函數(shù)![]() 當
當![]() 時,
時,![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
試題分析:(Ⅰ)利用等價不等式![]() ,進而通過解不等式可求得;(Ⅱ)根據(jù)條件可首先將問題轉(zhuǎn)化求解
,進而通過解不等式可求得;(Ⅱ)根據(jù)條件可首先將問題轉(zhuǎn)化求解![]() 的最小值,此最值可利用三角形不等式求得,再根據(jù)恒成立的意義建立簡單的關于
的最小值,此最值可利用三角形不等式求得,再根據(jù)恒成立的意義建立簡單的關于![]() 的不等式求解即可.
的不等式求解即可.
試題解析:(Ⅰ)當![]() 時,
時,![]() .
.
解不等式![]() ,得
,得![]() .
.
因此,![]() 的解集為
的解集為![]() . ………………5分
. ………………5分
(Ⅱ)當![]() 時,
時,![]()
![]()
![]() ,
,
當![]() 時等號成立,
時等號成立,

考點:1、絕對值不等式的解法;2、三角形絕對值不等式的應用.