2016年四川高考文科數學試題解析(word版
2016年高考四川文科數學
一、選擇題:本大題共10小題,每小題5分,共50分.在每小題給出的四個選項中,只有一個是符合題目要求的。
1.設i為虛數單位,則復數(1+i)2=
(A) 0
(B)2
(C)2i
(D)2+2i
【答案】C
【解析】
 (A)6 (B) 5 (C)4(D)3
(A)6 (B) 5 (C)4(D)3
【答案】B

考點:集合中交集的運算.
3.拋物線y2=4x的焦點坐標是
(A)(0,2)
(B) (0,1)
(C) (2,0)
(D) (1,0)
【答案】D
【解析】
 【答案】A
【答案】A
【解析】
![]() 故選A.
故選A.
考點:三角函數圖像的平移.
5.設p:實數x,y滿足x>1且y>1,q: 實數x,y滿足x+y>2,則p是q的
(A)充分不必要條件 (B)必要不充分條件
(C) 充要條件 (D) 既不充分也不必要條件
【答案】A
【解析】
![]() 充分不必要條件,選A.
充分不必要條件,選A.
考點:充分必要條件.
6.已知a函數f(x)=x3-12x的極小值點,則a=
(A)-4 (B) -2 (C)4 (D)2
【答案】D
 考點:函數導數與極值.
考點:函數導數與極值.
7.某公司為激勵創新,計劃逐年加大研發獎金投入。若該公司2015年全年投入研發獎金130萬元,在此基礎上,每年投入的研發獎金比上一年增長12%,則該公司全年投入的研發獎金開始超過200萬元的年份是
(參考數據:lg1.12=0.05,lg1.3=0.11,lg2=0.30) www.gaosan.com
(A)2018年(B)2019年(C)2020年(D)2021年
【答案】B
【解析】
試題分析:設從2015年后第n年該公司全年投入的研發資金開始超過200萬元,由已知得 考點:1.增長率問題;2.常用對數的應用.
考點:1.增長率問題;2.常用對數的應用.
8.秦九韶是我國南宋時期的數學家,普州(現四川省安岳縣)人,他在所著的《數書九章》中提出的多項式求值的秦九韶算法,至今仍是比較先進的算法。如圖所示的程序框圖給出了利用秦九韶算法求多項式值的一個實例,若輸入n,x的值分別為3,2,則輸出v的值為
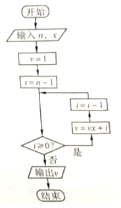
(A)35(B)20(C)18(D)9
【答案】C
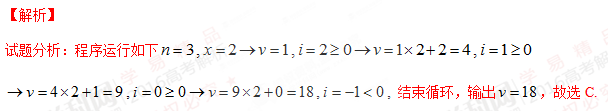
考點:1.程序與框圖;2.秦九韶算法;3.中國古代數學史. www.gaosan.com
 【答案】B
【答案】B

考點:1.向量的數量積運算;2.向量的夾角;3.解析幾何中與圓有關的最值問題.

考點:三角函數誘導公式
已知某三菱錐的三視圖如圖所示,則該三菱錐的體積 。www.gaosan.com
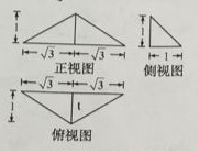
![]()

考點:1.三視圖;2.幾何體的體積.
從2、3、8、9任取兩個不同的數值,分別記為a、b,則![]() 為整數的概率= 。
為整數的概率= 。
【答案】1/6
【解析】
 時,定義“伴隨點”為它自身,現有下列命題:
時,定義“伴隨點”為它自身,現有下列命題:
?若點A的“伴隨點”是點![]() ,則點
,則點![]() 的“伴隨點”是點A.
的“伴隨點”是點A.
?單元圓上的“伴隨點”還在單位圓上。
?若兩點關于x軸對稱,則他們的“伴隨點”關于y軸對稱
④若三點在同一條直線上,則他們的“伴隨點”一定共線。
其中的真命題是 。
【答案】②③

考點:1.新定義問題;2.曲線與方程.
16、(12分)我國是世界上嚴重缺水的國家,某市為了制定合理的節水方案,對居民用水情況進行了調查,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數據按照[0,0.5), [0.5,1),……[4,4.5]分成9組,制成了如圖所示的頻率分布直方圖。
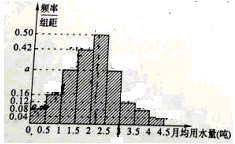
(I)求直方圖中的a值;
(II)設該市有30萬居民,估計全市居民中月均用水量不低于3噸的人數.說明理由;
(Ⅲ)估計居民月均用水量的中位數。
【答案】(Ⅰ)a=0.3;(Ⅱ)36000;(Ⅲ)2.04.

考點:頻率分布直方圖、頻率、頻數的計算公式
17、(12分)
如圖,在四棱錐P-ABCD中,PA⊥CD,AD∥BC,∠ADC=∠PAB=90°,BC=CD=?AD。
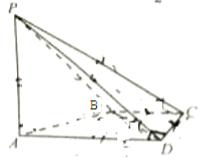
(I)在平面PAD內找一點M,使得直線CM∥平面PAB,并說明理由;www.gaosan.com
(II)證明:平面PAB⊥平面PBD。
【答案】(1)取棱AD的中點M,證明詳見解析;(2)證明詳見解析.
【解析】
試題分析:本題考查線面平行、線線平行、線線垂直、線面垂直等基礎知識,考查空間想象能力、分析問題的能力、計算能力.第一問,利用線面平行的定理,先證明線線平行,再證明線面平行;第二問,先由線面垂直得到線線垂直,在利用線面垂直的性質得到BD⊥平面PAB,最后利用面面垂直的判定定理證明面面垂直.
試題解析:
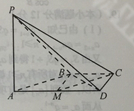


考點:線面平行、線線平行、線線垂直、線面垂直.
18、(本題滿分12分)
 【答案】(1)證明詳見解析;(2)4.
【答案】(1)證明詳見解析;(2)4.
【解析】
試題分析:本題考查正弦定理、余弦定理、商數關系等基礎知識,考查學生的分析問題的能力和計算能力.第一問,利用正弦定理,將邊角進行轉化,結合誘導公式進行證明;第二問,利用余弦定理解出cos A=3/5,再根據平方關系解出sinA,代入已知中,解出tanB的值.
 考點:正弦定理、余弦定理、商數關系
考點:正弦定理、余弦定理、商數關系
19、(本小題滿分12分)
已知數列{an}的首項為1,Sn為數列{an}的前n項和,Sn+1=Sn+1,其中q﹥0,n∈N+
(Ⅰ)若a2,a3,a2+ a3成等差數列,求數列{an}的通項公式;


 考點:數列的通項公式、雙曲線的離心率、等比數列的求和公式
考點:數列的通項公式、雙曲線的離心率、等比數列的求和公式
20、(本小題滿分13分)



考點:橢圓的標準方程及其幾何性質.
21、(本小題滿分14分)